JavaScript 中的 Tree 使用父指针高效遍历

前言

在本系列的第一部分中，我们研究了遍历二叉树的递归和迭代方法。在实际应用中，树节点有一个父节点是很常见的：一个指向父节点的指针，因此也称为父指针。让我们以浏览器中的 DOM 为例。假设我们使用以下命令选择任何节点：

const element = document.querySelector("#id")

在本文中，我们将研究如何使用这些父指针来提高遍历效率。我稍后会解释我所说的“更高效”是什么意思。在下一篇文章中，我们还将了解如何使用此处学到的经验教训从头开始创建 myQuery 库。

更新节点定义

首先，我们需要更新Node 函数

function Node(value){
  this.value = value
  this.left = null
  this.right = null
  this.parent = null // added parent field
}

现在让我们看看如何使用这个新的 Node 定义来创建一个类似的树，就像我们在上一篇文章中所做的那样。

const root = new Node(2)
const left = new Node(1)
root.left = left
left.parent = root

const right = new Node(3)
root.right = right
right.parent = root

我们只需要确保父指针指向父节点。这是我们使用上述代码获得的最终树的视觉参考：

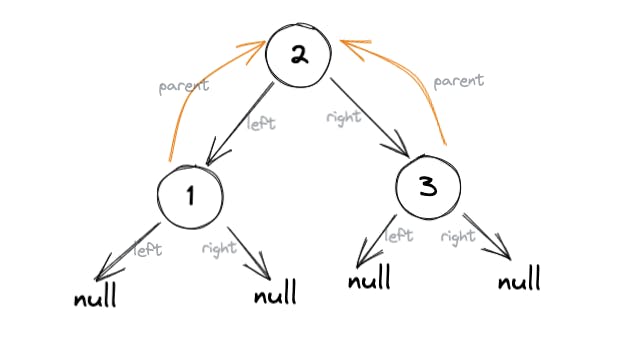
##寻找后继节点

前序后继

假设每个节点都有一个parent指针，如何找出二叉树中任何节点的前序后继？让我们试着分析一下这个问题：

首先，我们在这里处理前序，这意味着我们正在寻找以下顺序：

root -> left -> right

这意味着如果我们已经在当前节点，我们想寻找左子节点作为后继节点。
如果根本没有左子节点怎么办？那么在这种情况下，我们会寻找合适的节点，如果在有左子节点，那就是后继节点。
如果没有左子节点或右子节点，那么我们需要回溯（继续向上走向父节点）。我们一直回溯，直到通过它的右子节点到达父级（因为这意味着前序对于父级下的整个子树是完整的，根据 #1 的定义）。

最终算法实现就是这样：

function preOrderSuccessor(node){
   if(!node) return

   if(node.left) return node.left
   if(node.right) return node.right

   let parent = node.parent

   while(parent && parent.right === node) {
     node = node.parent
     parent = parent.parent
   }

   if(!parent) return null // we backtracked till root, so no successor

   return parent.right
}

可以根据下图更好的理解

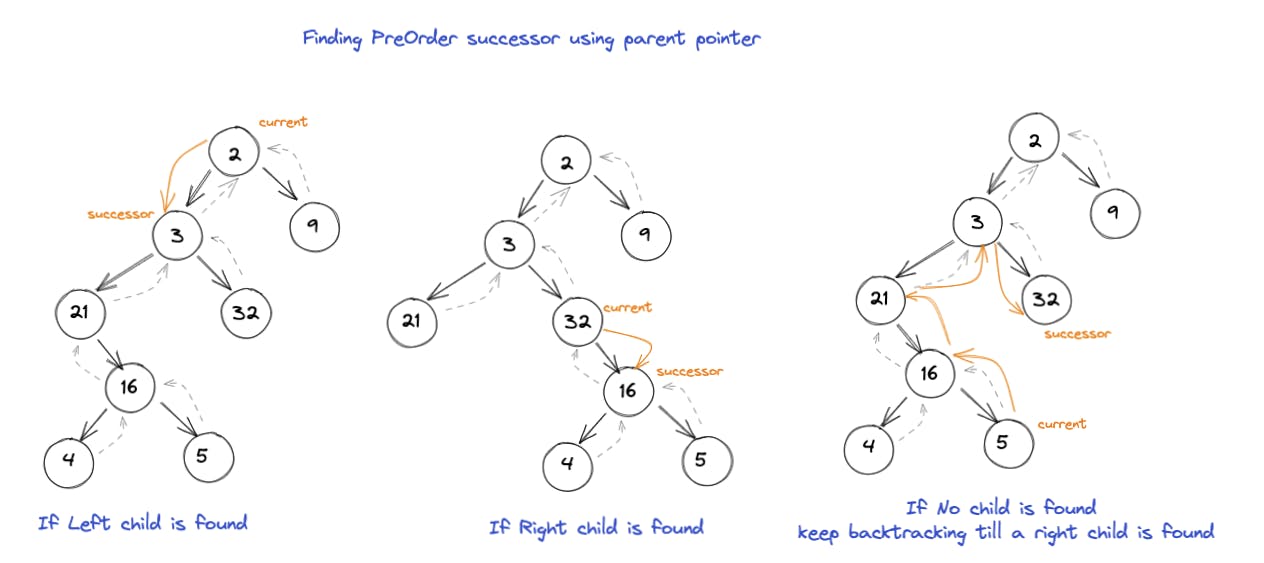
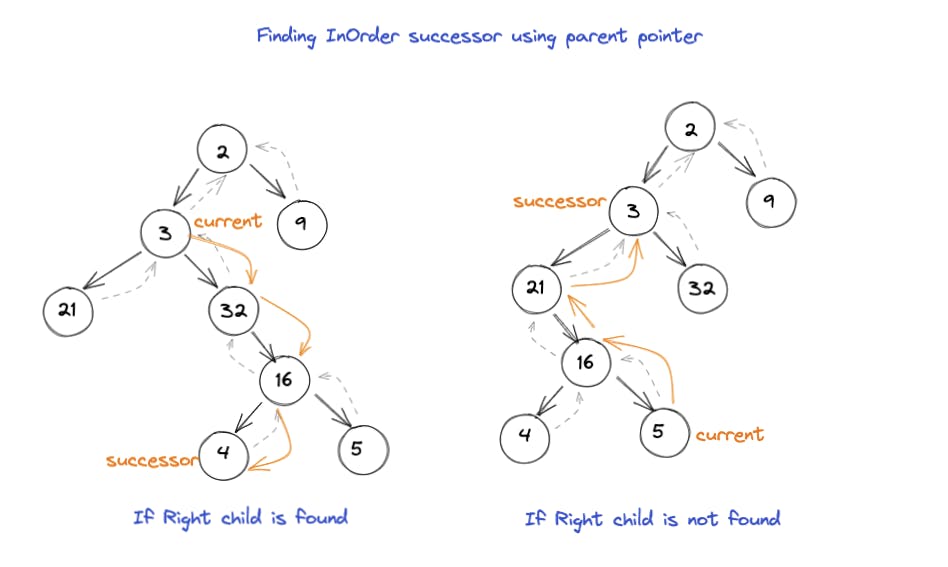
中序后继

首先，我们在这里处理中序遍历，这意味着我们正在寻找以下顺序：

root -> left -> right

如果我们在当前节点，并且它右边有右子节点，那么我们可以通过在右子树上找到最左边的节点来获得后继节点。
如果没有右子节点，那么我们需要回溯（向上移动）。我们一直向上移动，直到通过它的右子节点到达父节点，因为这意味着已经遍历了整个子树（根据 #1 中的定义）。
一旦我们找到最近的父节点，它是通过它的左子节点找到的，它就会作为后继节点返回。为什么？因为这意味着它是一个已经探索了左树的节点，所以根据 #1 中的定义，节点本身现在是后继节点。实现如下：

function inOrderSuccessor(node){
   if(!node) return

   if(node.right){
     let current = node.right
     while(current && current.left) current = current.left
     return current
   }

   let parent = node.parent

   while(parent && parent.right === node) {
     root = node.parent
     parent = parent.parent
   }

   if(!parent) return null

   return parent
}

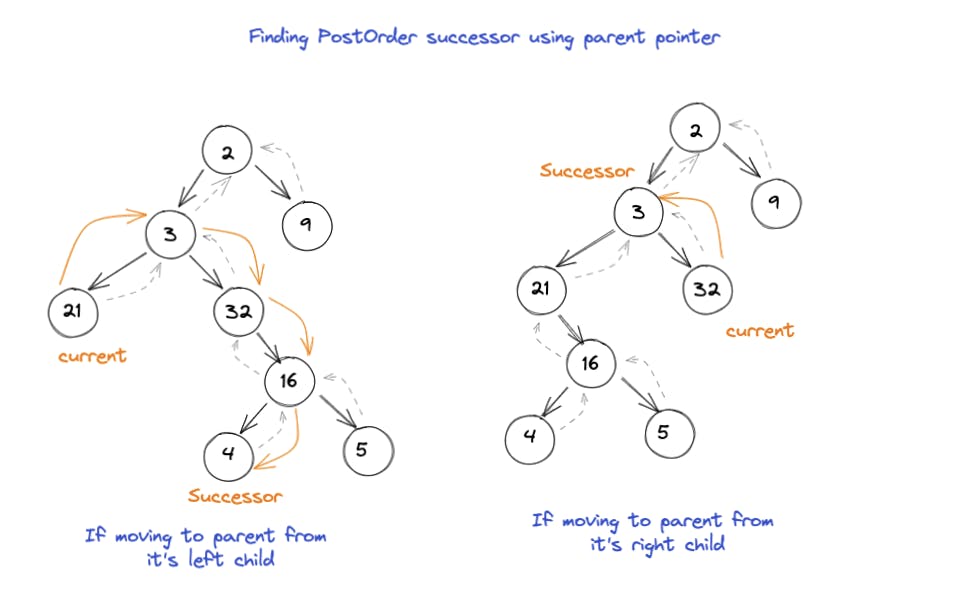
后序后继

首先，我们在这里处理后序遍历，这意味着我们正在寻找以下顺序：

left -> right -> root

所以，如果我们在任何节点上，就意味着它的左右子树已经被访问过了。这意味着我们需要查看父级的继任者。
如果我们从它的右子节点到达父母，这意味着父母本身就是继任者，根据#1 中的定义
如果我们从它的左子节点到达父母，这意味着接下来要探索父母的右子节点（根据#1 中的定义）。所以现在我们需要简单地返回父节点右子节点中最左边的节点作为后继节点。实现如下：

function postOrderSuccessor(node){
   if(!node) return

   let parent = node.parent
   if(!parent) return null

   if(parent.right === node). return parent

   let current = parent.right
   while(current && (current.left || current.right)){
     current = (current.left || current.right)
   }

   return current
}

使用后继算法更好地遍历

为什么我们需要使用父指针来提出遍历算法呢？这是一个值得思考的问题，因为我们已经提出了遍历树的递归和迭代方法，而且不需要父指针。

我们这样做的原因是因为我们之前的方法增加了空间复杂性。如果你还记得上一篇文章中我们需要使用一个或两个堆栈（取决于遍历方法）来使任何遍历算法工作。即使在递归方法中，虽然我们不直接使用堆栈，但递归本身基于调用堆栈，因此那里也使用了隐藏的内存中堆栈。问题是这个堆栈的大小会随着我们树的深度而增加，因此这不是最好的解决方案，因为我们有办法在花费更少空间的情况下完成相同的任务。通过使用父指针，我们可以完全摆脱这些堆栈，为我们节省大量空间，即从 O(logN) 的空间复杂度（其中 N 表示平衡树的大小）到 O(1)。让我们看看如何实现。

前序遍历

对于前序遍历，我们从树的根部开始。之后，我们可以使用上面的算法继续获取前序后继以遍历整棵树：

function preOrder(root){
  // first node
  console.log(root.value);

  let current = root
  while(true){
    const next = preOrderSuccessor(current)
    if(!next) break

    // do something
    console.log(next.value)

    current = next
  }
}

中序遍历

对于中序遍历，起始节点将是树的最左侧节点。此后，我们可以使用上述算法继续获取后继以遍历整棵树：

function inOrder(root){
  // start at the left most node
  while(root && root.left){
    root = root.left
  }

  // first node
  console.log(root.value);

  let current = node
  while(true){
    const next = inOrderSuccessor(current)
    if(!next) break

    // do something
    console.log(current.value)

    current = next
  }
}

后序遍历

非常类似于上面的中序遍历的方法：

function postOrder(root){
  // start at the left most node
  while(root && root.left){
    root = root.left
  }

  // first node
  console.log(root.value);

  let current = node
  while(true){
    const next = postOrderSuccessor(current)
    if(!next) break

    // do something
    console.log(current.value)

    current = next
  }
}

进阶

如果每个节点都有一个父指针，你能想出算法来寻找前任（inOrder、preOrder 和 postOrder）吗？

前言​

更新节点定义​

前序后继​

中序后继​

后序后继​

使用后继算法更好地遍历​

前序遍历​

中序遍历​

后序遍历​

进阶​

前言