JavaScript 中的 Heap
前言
之前我们已经研究了树数据结构的实现以及它的一些变体,例如 trie。在这篇文章中,我们将深入研究堆。它也称为优先级队列。
什么是堆?
堆是树数据结构的一种变体,具有两个附加属性:
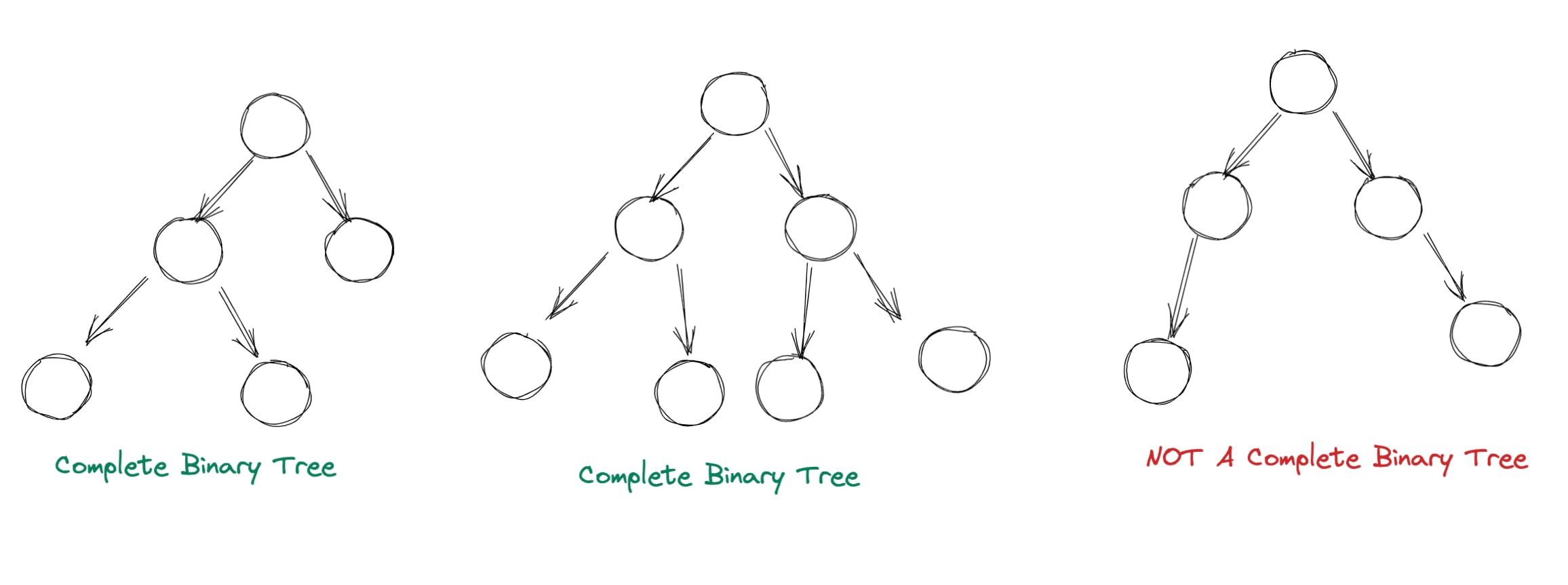
1.它是一棵完全二叉树:一棵完全二叉树的每一层都包含最大数量的节点,可能最后一层除外,它必须从左到右填充。完整的二叉树总是通过它的定义来平衡的。作为参考下图显示了什么时候可以将树称为完全二叉树:
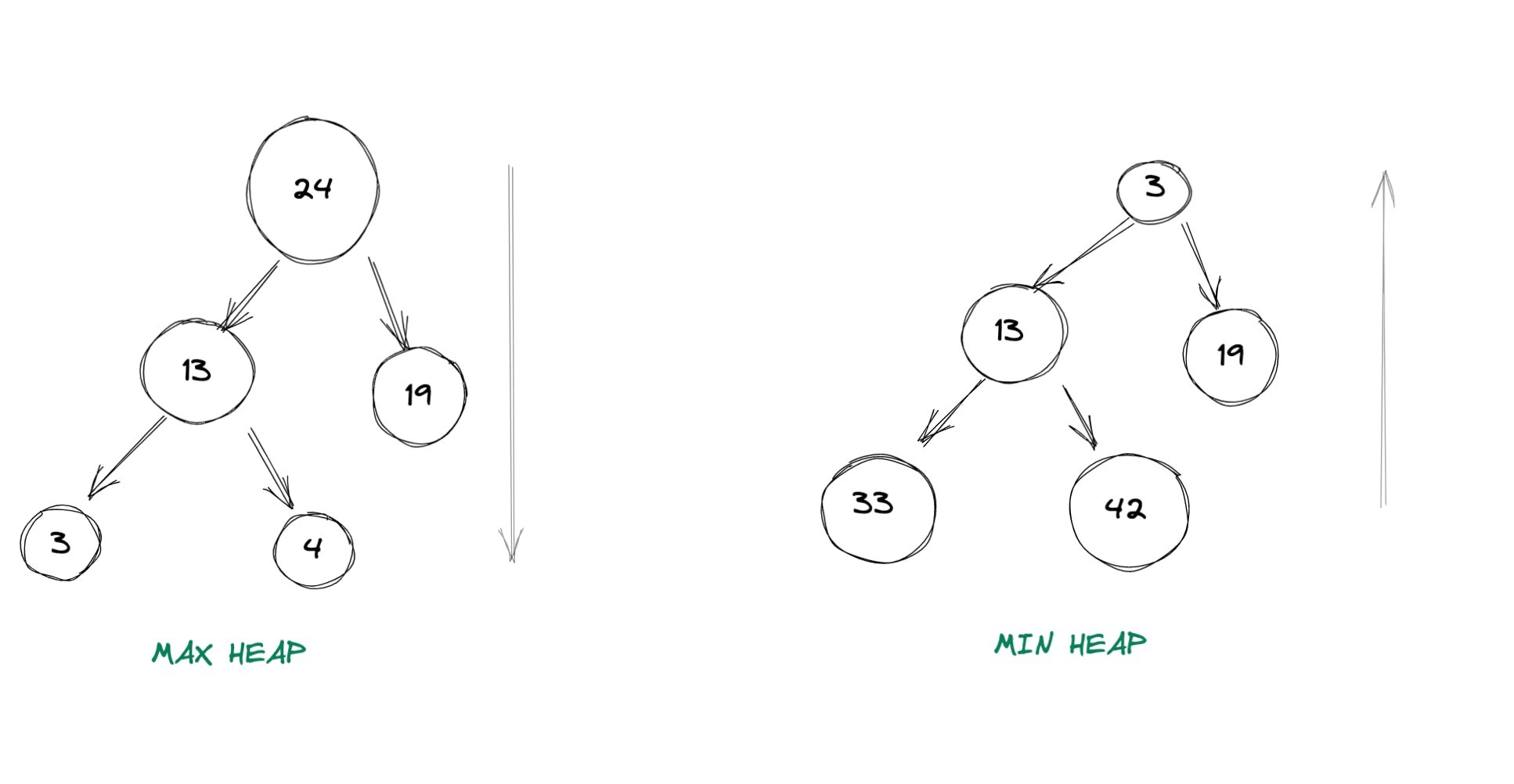
2.每个节点都满足“堆属性”:堆属性本质上意味着对于任何给定的节点 C,如果 P 是 C 的父节点,则:
- 对于最大堆:P 的键应该大于或等于 C 的键。
- 对于最小堆:P 的键应该小于或等于 C 的键。
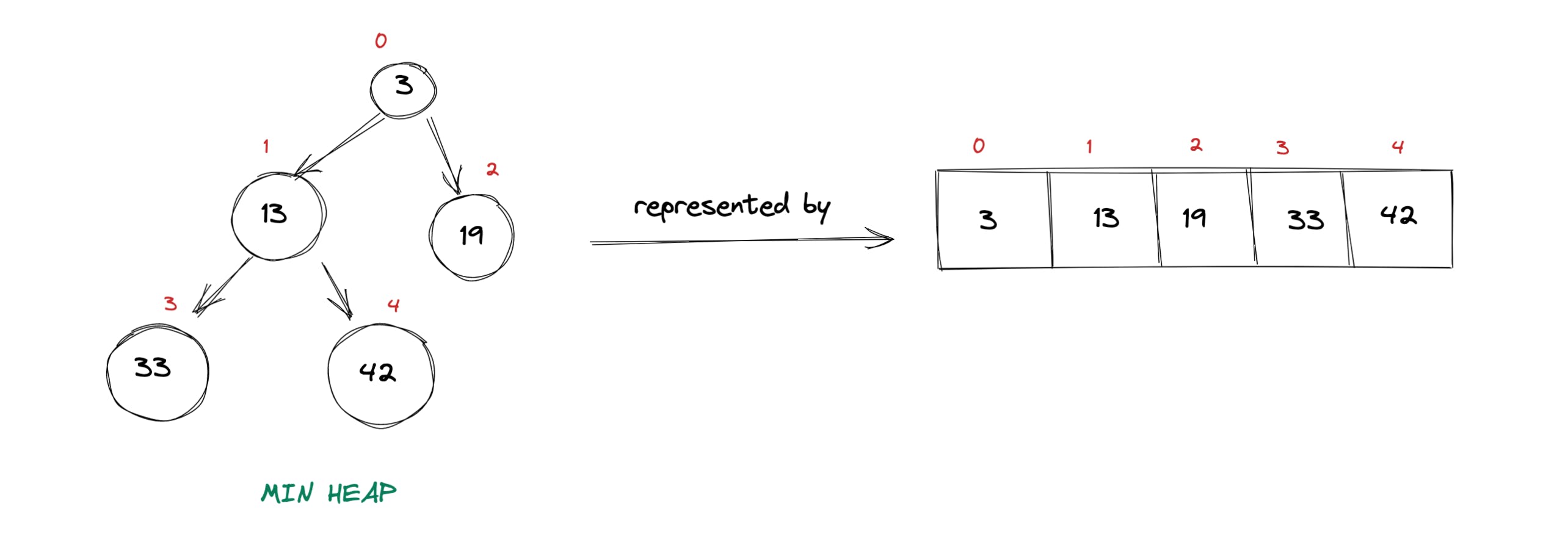
如何表示堆?
我们通常从节点的类表示开始实现,然后将其与实际数据结构本身的类表示联系起来。我们也可以对堆做同样的事情。但是,有一种更简单的方法可以解决此问题,这是因为所有堆都必须遵守以下两个属性之一:
所有堆必须是完全二叉树
由于所有堆都必须是完全二叉树,并且我们知道完全二叉树中除最后一层外的所有级别都必须完全填充。此外,对于最后一层,所有子项必须从左到右方向填充,没有任何间隙。这个定义确保了一个由 n 个节点组成的完全二叉树只能有 1 种可能的形状。反过来,它允许我们使用数组来表示完整的二叉树。这意味着,堆也可以使用数组来表示。例如,我们可以将一个简单的堆表示为一个数组,如下图所示:
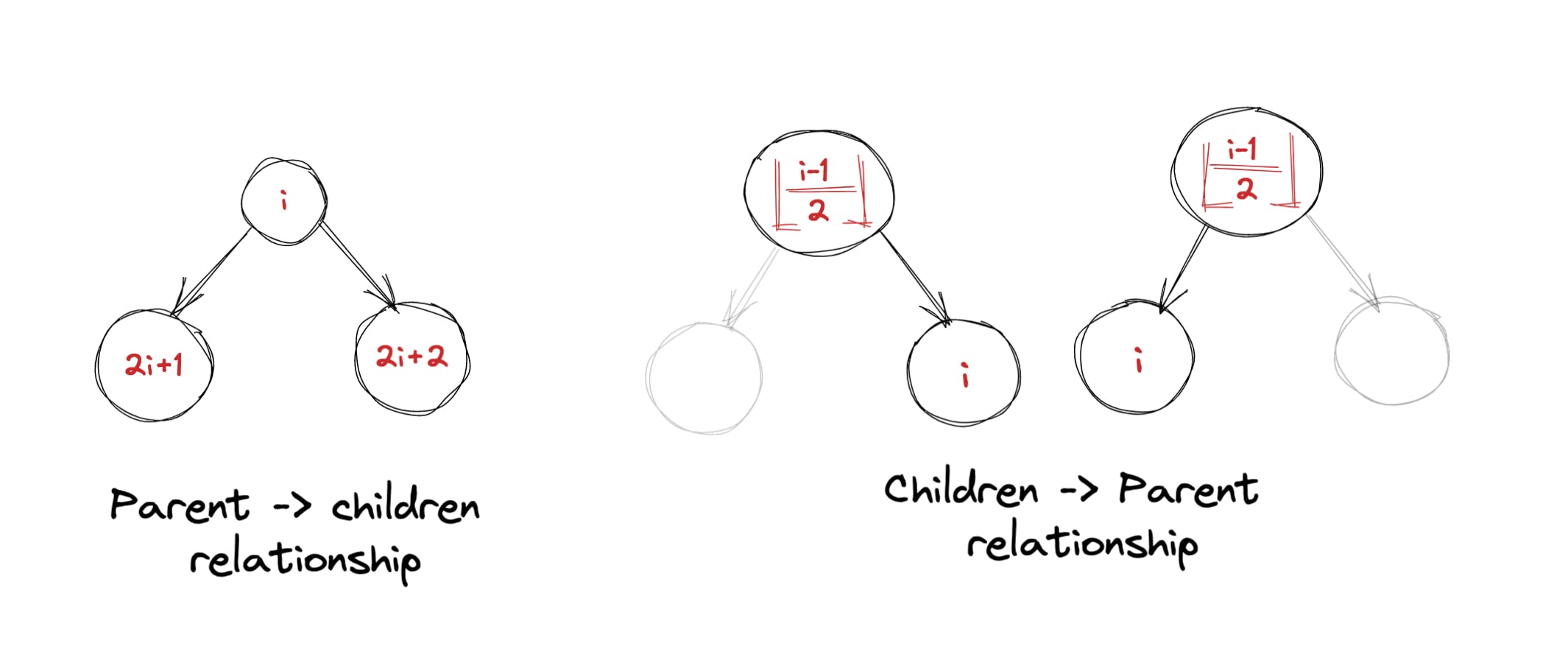
这里要注意的关键是父节点和子节点之间的关系。如果仔细观察上图,我们可以推断出以下内容:
- 如果节点位于数组中的索引 i 处,则假设结果索引位于数组的长度内:
- 它的左孩子将在第 (2i+1) 个位置
- 左孩子将在 (2i+2) 位置
- 如果一个节点被放置在数组中的索引 i 处,它的父节点将位于第 ((i-1)/2) 个索引处。
下图可以更轻松地使用上述信息:
具体实现
注意:在整个实现过程中,我们只会讨论最小堆。稍后我们将看到如何将相同的想法轻松扩展到最大堆。
在我们已经涵盖了表示的细节,让我们想出一个使用数据结构的接口。在堆数据结构的帮助下,我们希望能够实现三个关键点:
- 向堆中添加一个新键
- 从堆中删除最大或最小键(取决于它是最小堆还是最大堆)
- 从堆中获取最小键的最大值(取决于是最小堆还是最大堆)
第三个操作很简单。我们知道对于最小堆,数组中的第一项将是最小键,同样对于最大堆,数组中的第一项将是最大键。所以我们剩下两个操作的实现:
// adds the provided newKey into the min-heap named "heap"
function heappush(heap, newKey){}
// removes the smallest key from the min-heap named "heap"
function heappop(heap){}
实现heappush()
我们如何向堆中添加一个新键?假设我们首先将新键推送到数组中。推送新键仍然让我们遵守堆的第一个要求,即它必须是一个完整的二叉树。但是,我们需要确保它也遵守“堆属性”。
我们可以通过将push的项与其父项进行比较来做到这一点。如果父项大于的push的项,那么我们知道堆属性被违反,因此我们可以交换。我们可以继续进行这种交换,直到找到一个合法的父节点或者我们已经到达堆的顶部。
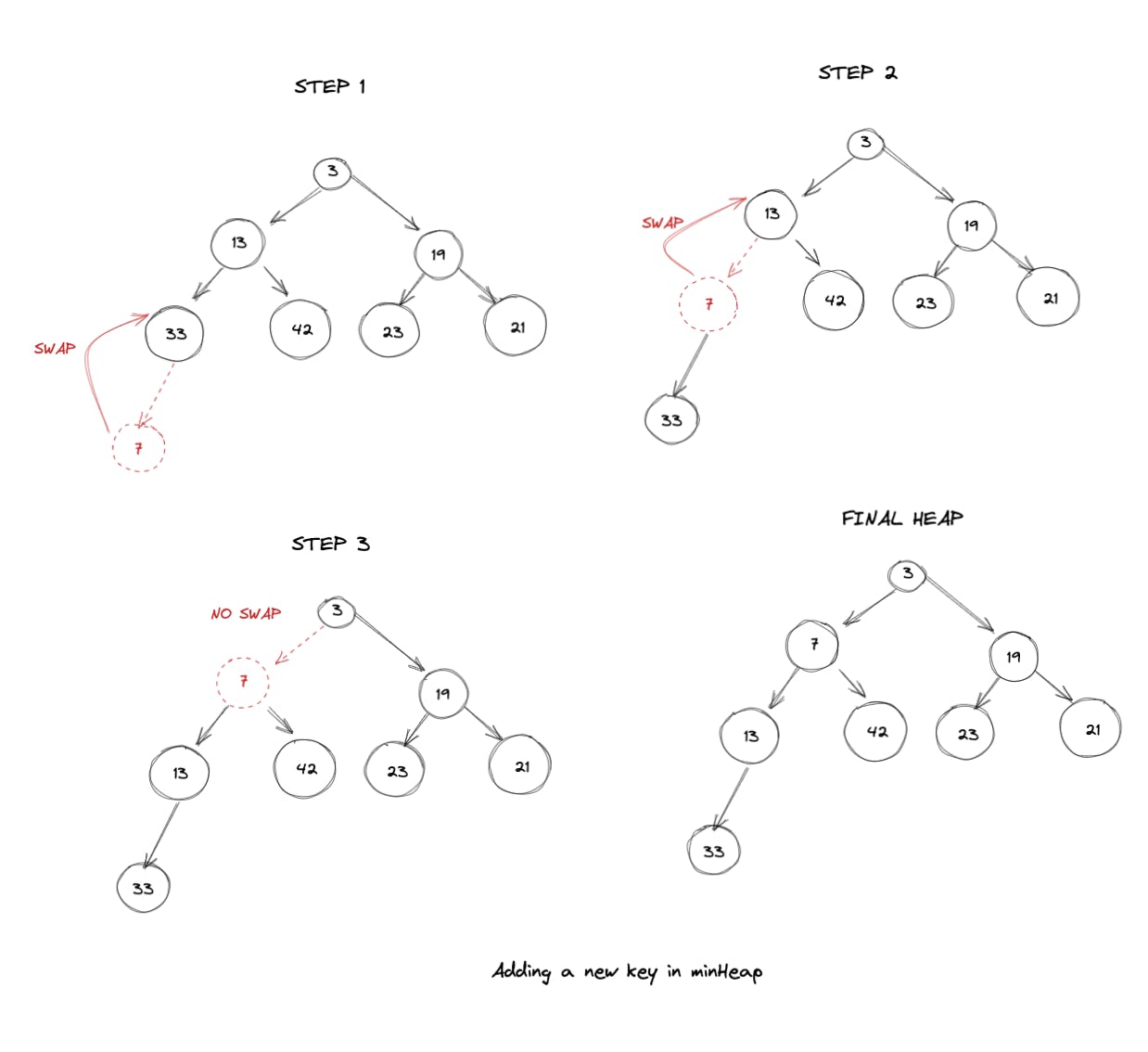
代码如下
function heappush(heap, newKey){
// push the new key
heap.push(newKey);
// get the current index of pushed key
let curr = heap.length-1;
// keep comparing till root is reached or we terminate in middle
while(curr > 0){
let parent = Math.floor((curr-1)/2)
if( heap[curr] < heap[parent] ){
// quick swap
[ heap[curr], heap[parent] ] = [ heap[parent], heap[curr] ]
// update the index of newKey
curr = parent
} else{
// if no swap, break, since we heap is stable now
break
}
}
}
实现 heappop()
使用 heappop() 我们需要删除堆的最顶层元素。意思是,对于最小堆,最小键将被删除,而对于最大堆,最大键将被删除。从数组的角度来看,它只是意味着我们应该删除数组的第一项。但是哪个节点应该成为根?如果我们随机选择被移除节点的左孩子或右孩子作为新的根节点,则不能保证遵循堆属性。我们可以按照以下步骤(对于最小堆):
- 将根节点与最后一个节点交换(数组中的第一个元素与最后一个元素)
- 通过从数组中弹出最后一项来删除根节点
- 将新根节点的键与其子节点进行比较:
- 如果键小于它的两个子键,则堆是稳定的
- 否则,将Key与较小的子Key交换
- 重复步骤 3,直到到达最后一个子节点或建立堆属性。
本质上,我们遵循与 heappush() 类似的过程,除了我们试图以从上到下的方式建立堆属性,即从根开始并一直持续到最后一个孩子。在 heappush() 中,我们遵循相反的顺序,即从最后一个孩子开始,一直到根。
代码实现:
function heappop(heap){
// swap root with last node
const n = heap.length;
[heap[0], heap[n-1]] = [ heap[n-1], heap[0]]
// remove the root i.e. the last item (because of swap)
const removedKey = heap.pop();
let curr = 0;
// keep going till atleast left child is possible for current node
while(2*curr + 1 < heap.length){
const leftIndex = 2*curr+1;
const rightIndex = 2*curr+2;
const minChildIndex = (rightIndex < heap.length && heap[rightIndex] < heap[leftIndex] ) ? rightIndex :leftIndex;
if(heap[minChildIndex] < heap[curr]){
// quick swap, if smaller of two children is smaller than the parent (min-heap)
[heap[minChildIndex], heap[curr]] = [heap[curr], heap[minChildIndex]]
curr = minChildIndex
} else {
break
}
}
// finally return the removed key
return removedKey;
}
使用现有数组创建堆
从现有数组创建堆看起来非常简单。只需创建一个空堆,然后遍历数组的所有项并执行 heappush():
function heapify(arr){
const heap = []
for(let item of arr){
heappush(heap, item)
}
return heap;
}
但是我们可以在这里做得更好吗?是的。首先,我们可以完全避免为新堆使用额外的空间。为什么不重新排列数组本身的元素,使其满足堆属性?为此,我们可以遵循与堆弹出类似的逻辑。我们可以查看第一个节点并与它的子节点进行比较,看看它是否是最小的节点,如果不是与较小的子节点交换。下面我们来实现一下:
// follows pretty much the same logic as heappush, except minor modifications
function percolateDown(heap, index){
let curr = index;
// keep going down till heap property is established
while(2*curr + 1 < heap.length){
const leftIndex = 2*curr+1;
const rightIndex = 2*curr+2;
const minChildIndex = (rightIndex < heap.length && heap[rightIndex] < heap[leftIndex] ) ? rightIndex :leftIndex;
if(heap[minChildIndex] < heap[curr]){
// quick swap, if smaller of two children is smaller than the parent (min-heap)
[heap[minChildIndex], heap[curr]] = [heap[curr], heap[minChildIndex]]
curr = minChildIndex
} else {
break
}
}
我们可以对数组中的所有元素使用 percolateDown() 函数,按照堆属性将所有元素按正确顺序排列:
function heapify(heap){
for(let i in heap){
percolateDown(heap, i)
}
return heap
}
这样就为我们节省了一个额外的数组。但是我们能做些什么来改善所花费的时间吗?是的。如果你仔细观察,我们实际上是在做一些重复的工作。假设堆中有 n 个节点,其中 x 是叶节点,那么这意味着我们只需要对 n-x 个节点执行 percolateDown(),因为到那时最后 x 个节点将在正确的位置。
那么在堆的数组表示中,我们应该执行 percolateDown() 操作到哪个索引?
直到最后一个节点的父节点所在的索引。因为一旦最后一个节点的父节点被过滤掉,它也会处理最后一个节点。所以:
- 如果数组长度为 n
- 最后一个节点的索引是:n-1
- 它的父节点的索引是:
Math.floor((n-1) - 1 / 2) = Math.floor(n/2 - 1)
function heapify(heap){
const last = Math.floor(heap.length/2 - 1);
for(let i = 0; i <= last; i++){
percolateDown(heap, i)
}
return heap
}
时间和空间复杂度
查看 heappush() 和 heapop() 操作,很明显我们在尝试添加或删除键时正在遍历树的高度。由于堆是一棵平衡树,因此高度是 log(n),其中 n 是节点总数。因此,对于堆的推送和弹出操作,时间复杂度为 O(log(n))。 heapify() 操作的时间复杂度可能看起来像 Onlog(n),因为每次调用都需要 O(log(n))。这个观察结果对于推导 heapify() 的时间复杂度的上限是正确的,但是,渐近(平均)时间复杂度为 O(n)。更多细节在这里。就空间复杂度而言,它是恒定的,因为额外的空间仅被诸如 curr、leftIndex 等大小恒定的变量占用。
最大堆
如果我们有 minHeap 的实现,我们也可以轻松地将它用作最大堆。我们只需要确保在向堆添加值时我们插入键的负数。它将确保堆充当所有键的负数的最小堆,这相当于所有实际键的最大堆。例如:
- 假设我们有一个数组
const x = [23, 454, 54, 29]; - 可以使用以下方法创建最小堆:
const heap = [];
for(let el of x) heappush(heap, el);
// min value
const min = heappop(heap)
最大堆可以使用
const heap = [];
for(let el of x) heappush(heap, -el);
// max value
const max = -heappop(heap)